2つの三角形がぴったり重なるかどうか、
それを数学的に証明をする練習を行うのがこの単元です。
このページでは
① 合同条件の確認
② テンプレートを使って証明する
の2つをご紹介します。
このページを読んだおかげで
証明が書けるようになった!
と言ってもらえることを目的としています。
では早速始めましょう!
合同条件のまとめ
早速合同条件から解説していきます。
①3組の辺がそれぞれ等しい
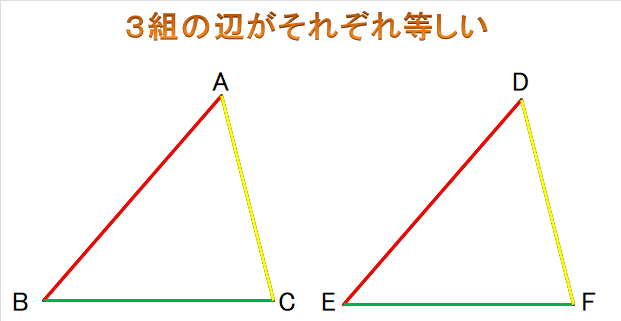
最初に習う合同条件の1つ目が
・3組の辺がそれぞれ等しい
という合同条件ですが、
これはどういうことかというと、
2つの三角形で、
全く同じ長さの辺が3組ある
ということです。
② 2組の辺とその間の角がそれぞれ等しい
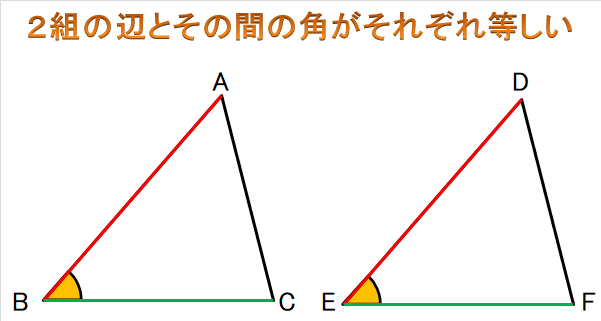
2つ目が
・2組の辺とその間の角がそれぞれ等しい
です。
どういう状態になっていたらこの条件に当てはまるのかというと
辺の長さが2組同じ長さであること
その2つの辺によってできる角の大きさが同じであること
この2つがどのような向きになっていても成り立てばいいのです。
(例)
例えば上図で辺ABと辺DEの長さが8cmで
辺BCと辺EFの長さが7cmだった場合、
2組の辺の長さが等しいので1つ目の条件クリアです。
もう1つの、∠Bと∠Eが40°だったとしたら、
この合同条件にぴったり当てはまる、
ということになります。
③ 1組の辺とその両端の角がそれぞれ等しい
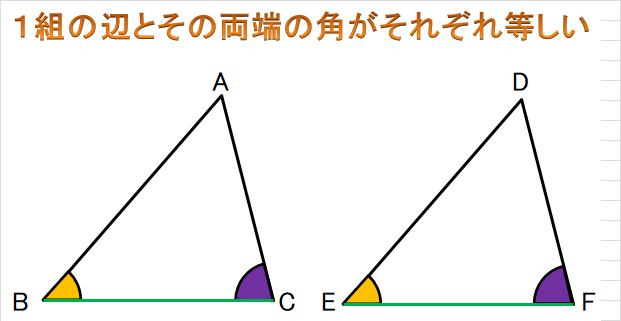
3つ目が
・1組の辺とその両端の角がそれぞれ等しい
です。
これはどういう状態であればいいのか、というと
2つの三角形で、とにかくどの辺でもいいので
長さの等しい辺が1くみある。
その辺の両側にある角の大きさが、2組とも
同じ大きさである
ということ。
(例)
例えば、上図でBCとEFのながさがどちらも5cmだったとします。
∠Bと∠Eが40°で∠Cと∠Fが75°だったとします。
そうすると、この1組の辺とその両端の角がそれぞれ等しい
という合同条件に当てはまります。
直角三角形の合同条件も一緒に覚えよう!
合同条件
と聞いたら、上記の①~③のことと思っている学生が多いのですが、
私は、指導している受講生に対して
合同条件は5つある!
と、いつも言っています。
直角三角形の合同条件を別扱いにするからみんなは、
「この合同条件はまた別モノなんだ!」
と思うことがそもそもややこしくしている原因だと思っています。
今日からこの記事を読んでいるみなさんは、
合同条件は5つ!
を合言葉に勉強に臨んでもらいたいと思います。
④ 直角三角形の斜辺と他の1辺がそれぞれ等しい
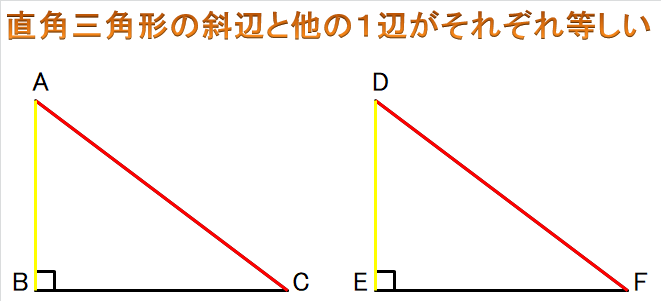
斜辺とは、
直角(90°)の角に向かい合っている辺(対辺)のことで、
上図でいうと、
90°が∠Bと∠Eなので、それに向かい合う辺が辺ACと辺DFということです。
また、他の1辺に関しては、上図の辺ABと辺DEが同じでもいいし、
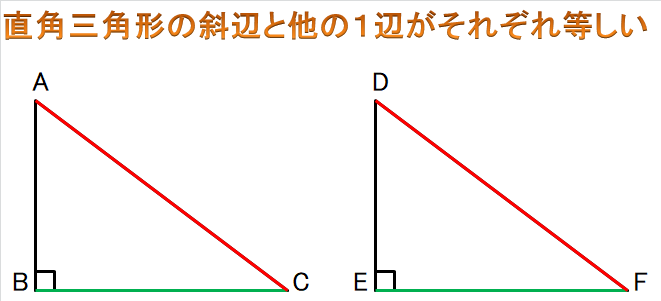
上図のように辺BCと辺EFの長さが同じでもOK。
間違えちゃいけないのは
90°が同じ
というのは既にわかっていることなので、
条件の中に含まないということ!
気を付けましょう!
⑤ 直角三角形の斜辺と1つの鋭角がそれぞれ等しい

先ほどと同じで、
90°は放っておきます。
90°の向かい合っている辺、
上図では辺ACと辺DFの長さが同じで、
∠Cと∠Fが同じ大きさであれば、この条件に当てはまります。
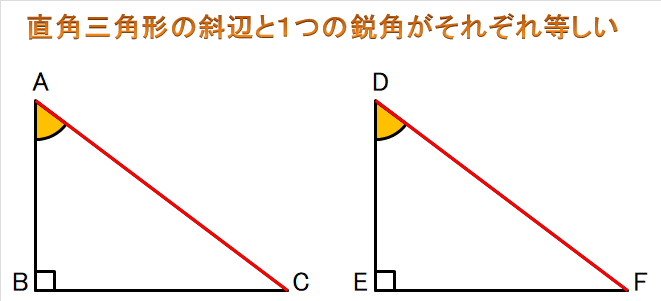
角に関して
絶対に∠Cと∠Fが同じでないとダメなの?
ということは無く、
∠Aと∠Dが同じであってもこの条件に当てはまります。
ということで、合同条件のまとめはこの辺で終わります。
合同証明の実践
では実際の合同の問題を解いてみます。
なお、この解き方は、基本テンプレートになるので、
この書き方をマスターして合同問題を得意分野にしましょう!
(問題)
下の図で、辺AE=辺DE、辺BE=辺CEのとき、
△ABE≡△DCEであることを証明しなさい。

証明の基本テンプレート
【証明】
△____と△____において ←必ず証明する図形を書く
仮定より ←仮定とは問題文に書かれている条件のこと
辺____=辺____ ・・・① 問題文に書かれている条件を
辺____=辺____ ・・・② そのまま使えばOK
___角は等しいので 角の大きさは、条件に書かれていないので
∠____=∠____ ・・・③ 自分で見つけ出すこと。
①~③より
___________がそれぞれ等しいので ←上記の①~③がこの合同条件になっている
△____≡△____
以上、証明終わり。
公式や裏技をもっと知りたい!
という方にお勧めの本を最後にご紹介します!
この本は、学習塾で専門の先生方が教えてくれる
「裏技」
がたくさん収録されています。
自分で勉強するときも参考書として使えるので便利です。
手元に是非1冊お求めください!