【2020奈良】数学　公立高校入試問題　大問４(３)

問題はこうだ！
解説は（３）だけです！
（３）①　解説です。
（３）②　解説です。

問題はこうだ！

解説は（３）だけです！

なんで（３）だけやねん！
はい、（１）からほんまは書きたかったんですが、知り合いのお子さんが、（３）だけ解き方わからんらしい、という情報を聞きつけ、実際に解いてみると、確かに、（３）の②は、ほんまにどないしよう？と悩んだもんで、いろいろ考えた挙句の攻略方法をここでご紹介しようと思って（３）だけに絞りました。（理由になりましたかね。）

（３）①　解説です。

図のままでは長さを求めるのはちょっと苦しいでしょうか。私は一本、線を付け足しました。
それがこれです↓

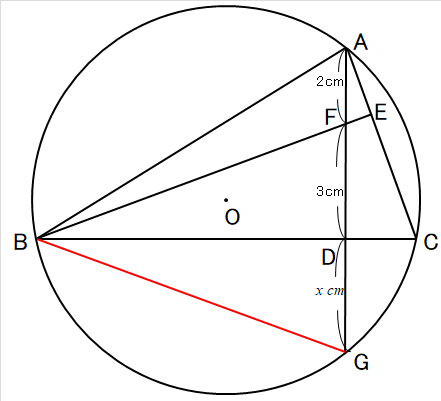
線分BGを引いた瞬間に、な～んとなく線分FDと長さが同じ感じやなあ、って思いましたね。
△BFDと△BGDの合同が証明出来たら線分FDと同じ長さになるので、ちょっとやってみようかな～って感じで始めました。

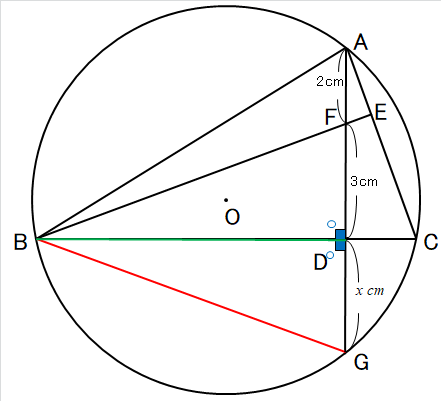
まず、∠BDF＝∠BDG＝９０°・・・①
次に、線分BDは共通で使われているので同じ長さですね。・・・②
さて、もう一つ、どこが同じやねん・・・、ん？ここか？！

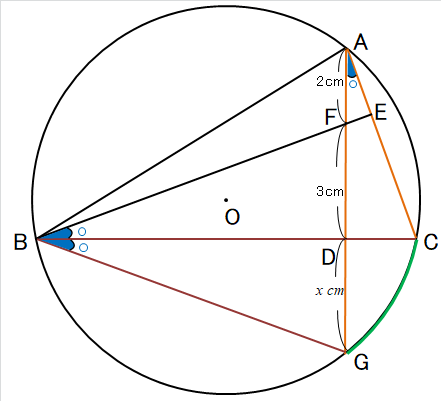
弧CGの円周角で、∠CAG＝∠CBG
さらに、（１）で△AFE∽△BCEが証明されているので、対応する角の大きさは等しいです。
よって∠EAF＝∠EBC
ここで、∠CAGと∠EAFは同じ角のことを言ってますよね。
だ・か・ら・・・
∠DBF＝∠DBG

おっ！合同できたやん！
一辺とその両端の角がそれぞれ等しい！

はい、線分DG＝３ｃｍ　確定しました！

（３）②　解説です。

これ、ちょっとむずかったですねぇ。
なんせ、円の面積を求めるわけなんで、半径の長さを求めんといかんのですわ。
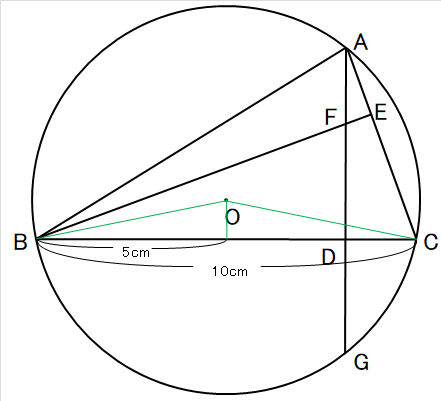
だから、一回目こんな線を引いてみたんですわ。

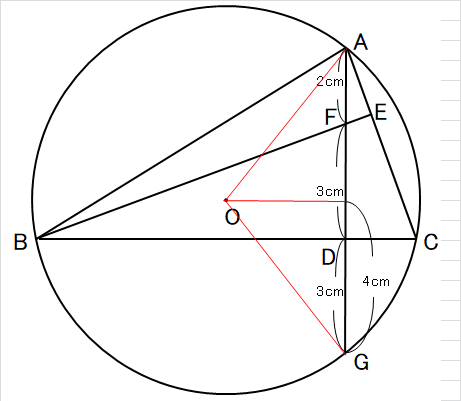
線分OA=線分OG＝半径だから、中心OからAGに垂線を引き下ろしたら線分AGが半分になるんで４ｃｍかぁ。
な～んか垂線と線分FDの長さが同じように見えるなあ。
これって、３：４：５の直角三角形なんかなぁ？
ということは、半径は５ｃｍで面積は２５\(\pi㎠\)か？
と思ったら、２６\(\pi㎠\)でした。

ほんなら３：４：５とちゃうか・・・。
どっかで聞いたことあるようなフレーズをつぶやきながら別の考え方を探す。
線分BCが１０ｃｍなんだよね。
一回こっちで考えるか。

これ書いた時点で、半径が５ｃｍとちゃうことがはっきりわかりますよね。
３：４：５なんて考えた私がアホでしたわ。
でもこの絵からも解決策が見えず、途方に暮れて・・・いなかったんですわ。
な～んでか。
それはね、

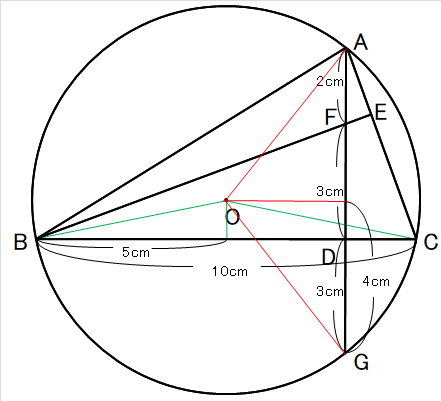
印刷した問題の挿絵がこういう感じになってたんですね。
この絵の中に、衝撃的な図形が隠れていたんですわ。
それがこちら↓

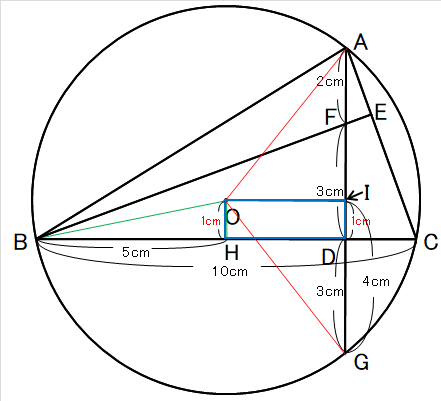
青線で囲んだ図形が長方形で、線分IDの長さが１ｃｍだとわかったんですね。
これ、緑の三角形と赤の三角形が重なってなかったら、ひらめかんかったと思います。
これにより、線分OHが１ｃｍになったので、半径である線分OB＝\(\sqrt{~26~}\)cmであることがわかりました。
なるほど、面積は\(\sqrt{~26~}\)×\(\sqrt{~26~}\)×\(\pi\)＝２６\(\pi㎠\)

ということで、普段の指導で、いらん線はいっぱい引くな！と指導してたんですが、いらん線が重なって解法にたどり着く、指導者泣かせの問題だなあ。みんな頑張って解いてね。