今回は、2021年3月10日に実施された
愛知県公立高校入試 B日程
の数学の問題の解説を行います。
まず最初に扱うのは
大問3(2)の図形の問題です。
なんてことない問題なのですが、
私なりの解法を載せておきますので
学習の参考になさってください。
なお、愛知県は、
学習範囲を制限せずに、全ての範囲を
出題範囲としています。
大問3(2)解法
まず問題を書きます。
図で、四角形ABCDは正方形であり、Eは辺DCの中点、
Fは線分AEの中点、Gは線分FBの中点である。
AB=8cmのとき、次の①、②の問いに答えなさい。
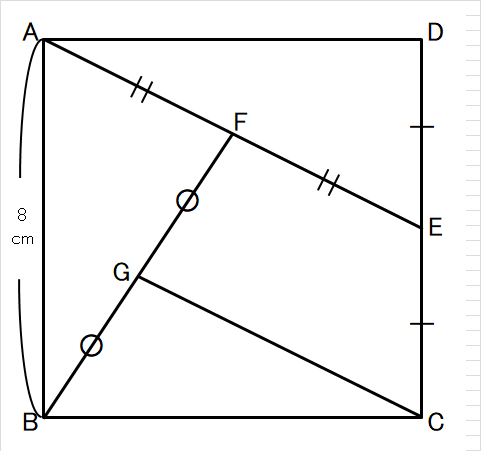
① 線分GCの長さは何㎝か、求めなさい。
愛知県は、三平方の定理を使う問題も
出題しているので、とりあえず
三平方を使えば解けるかな?
と、思いながら考えておりました。
まず、△ADEと△BFAの相似を考えました。
∠AED=∠BAF ですが、
EA:ABの線分比と
ED:AFの線分比が違うので、
△ADEと△BFAは相似では無いのです。
ということは、△BFAは直角三角形では無い、
ということになります。
ここで何を考えたのかというと、
AE//GCに何とかできないか?
ということです。
そうすると、下の図をご覧ください。
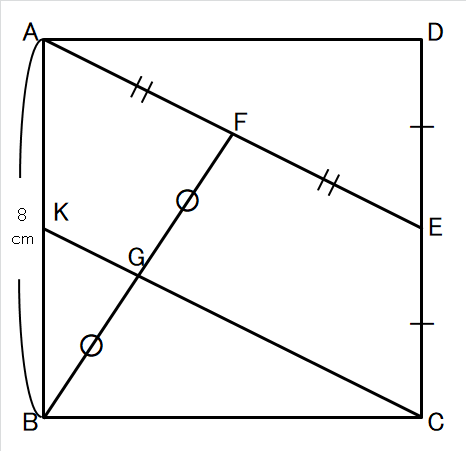
GCを延長させて、ABとの交点をKとすると、
四角形AKCEが平行四辺形になって、
△ADE≡△CBKとなって、
さらに中点連結定理が使えるので
KG=\(\frac{~1~}{~2~}\)AF
お!これは行けるぞ!
でもどうやってAE//GCを証明しようか・・・。
そう思いながら、ふっと正方形外に三角を書いてみた。
それが下の図です。
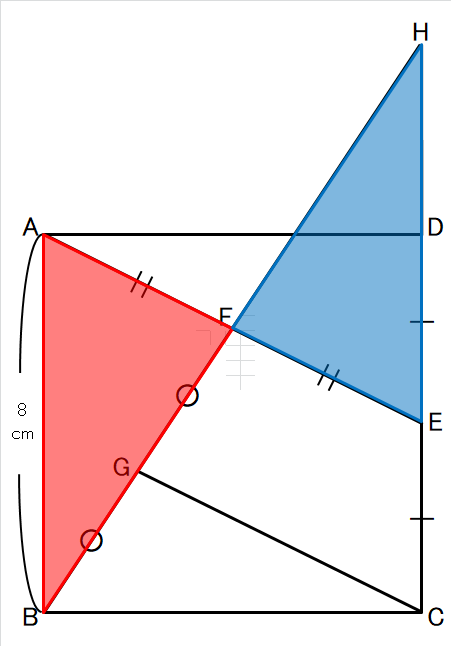
赤の三角形と青の三角形は合同になります。
これによって、先ほどの解法計画が一転しました。

HF=BF=(2○)
HE=AB=8㎝
これによって、
△HEFと△HCGが相似な図形になりました。
相似比は△HEF:△HCG=2:3
EFの長さは\(\frac{~1~}{~2~}\)AE
AEの長さは、三平方の定理より\(4\sqrt{~5~}\)を出せるので、
EFの長さは、\(2\sqrt{~5~}\)となります。
後は比でCGの長さを求めるだけ。
2:\(2\sqrt{~5~}\)=3:GC
GC=\(3\sqrt{~5~}\)
ということでした。
② 四角形FGCEの面積は何㎠か、求めなさい。
この問題は、青三角形の面積がわかれば
すぐに面積が求められる仕組みになっています。
まあ、三平方を使えば長さがわかるし・・・
えっ?この三角形って直角三角形じゃ無かったよね。
ではどうやって長さを出すんだよ!
下の図をご覧ください。
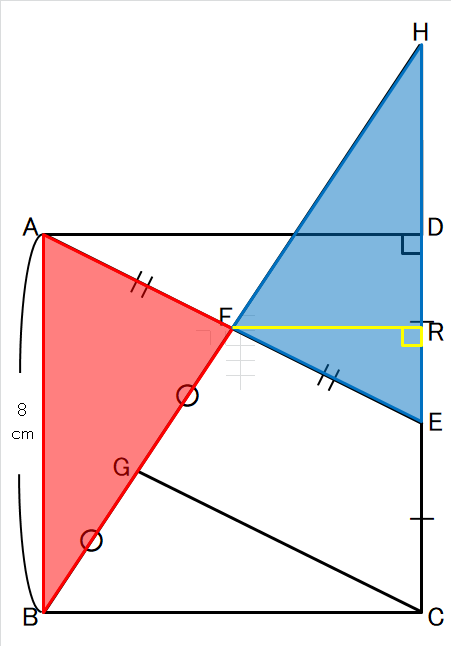
FからHEに垂線FRを引きます。
これが、△FHEの高さになりますよね。
次に、△ERF∽△EDAになりますね。
これでFRの長さを求められますね。
中点連結定理より、
FR=\(\frac{~1~}{~2~}\)AD=4㎝
これで△HEFの面積は8×4÷2=16㎠
が出ました。
次は、△HFEと△HGCの相似比から面積を求めて
四角形FGCEに持って行きましょう!
△HFEと△HGCの面積比は、相似比の2乗なので
4:9
これを利用して、
△HFEと四角形FGCEの面積比は4:5になりますね。
4:5=16:四角形FGCE
これより四角形FGCEの面積は20㎠
となります。
まとめ
この問題で押さえるべきは、
枠外にも三角形を作ってみる
ということです。
数学の問題解法で
「多分ここは平行」
なんてことはないんです。
ちゃんと平行の根拠を示して問題を解く、
これこそが数学の根本です。
そのためには公式や定理を頭に入れる必要があります。
そこでお勧めするのがこの本!
この塾技は、
公式や定理が凝縮されている「受験必勝本」
と言っても過言ではありません。
絶対に一人1冊は持っておくべきものと
思うくらい、貴重なものです。
是非お手元に一冊お買い求めください。