【2020年　大阪】数学　公立高校入試問題　C問題　大問３　解法

（１）①　解法

問題は、実際にホームページからダウンロードしたり、過去問を見てくださいね。では早速（１）①の解説から。

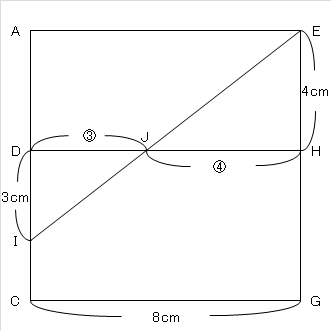
①は、△EJHの面積を求めろ、という問題。
そこで、面ADHEと面DCGHを一面にして、線分EIを引いてみる。
この時、△JDIと△JHEが相似な三角形となるので、相似比を探します。
DI：HE＝３：４なので、JD：JH＝３：４
欲しいのはJHの長さなので、
\(
JH＝８×\frac{~4~}{~7~}＝\frac{~32~}{~7~}cm
\)
△EJHの面積は、
\(
４×\frac{~32~}{~7~}×\frac{~1~}{~2~}=\frac{~64~}{~7~} cm^2
\)

（１）②　解法

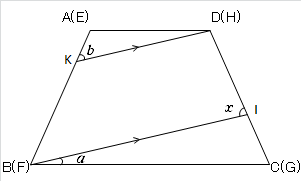
∠BID の大きさをa ，b を用いて表せ、という問題ですが、この問題を解くポイントは、二つの等脚台形を重ね合わせて１枚物として扱うことです。では、下の図をご覧ください。

• 

二つの等脚台形を重ね合わせました。
条件より、KH//BI
これにより、∠EKH＝∠ABI＝ｂ°
等脚台形の性質として、二つの底角は同じ大きさになるので、
∠ABC＝∠DCB＝\((a+b)\)°
さらに、△BCIに注目し、∠\(x\)=∠IBC+∠BCI
よって∠\(x\)=\(a+(a+b)=(2a+b)\)°

（１）③　解法

線分KF の長さを求めろ、という問題。
コイツにはちょっと苦戦しましたねぇ（笑）。
実はこの問題のヒントが（２）の図を見て得られました。
それでは図をご覧ください。

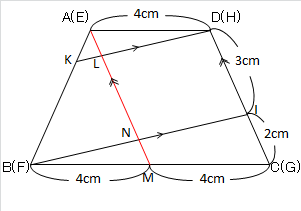
BCの中点をMとします。
（２）では、線分DMを引いていますが、これが問題解決に役立ちました。
先ほどの②の図をそのまま使用しますが、新たに赤線を一本引きました。
線分KH、線分BIと線分AMとの交点をそれぞれL、Nとします。
四角形LNIDは向かい合う２組の辺が平行なので平行四辺形になります。
よって、LN＝３cm
さらに、△BCI∽△BMNに気づきましたか？
中点連結ているが使えるので、NMの長さはあっという間に１cmが出るでしょう。
そうすると、残ったALの長さが１cmであることも判明します。
△ABN∽△AKLなので、A(E)K：KB(F)＝AL：LN＝１：３
KF＝５×\(\frac{~3~}{~4~}＝\frac{~15~}{~4~}\)cm

（２）①　解法

まず、図から見てみましょう。

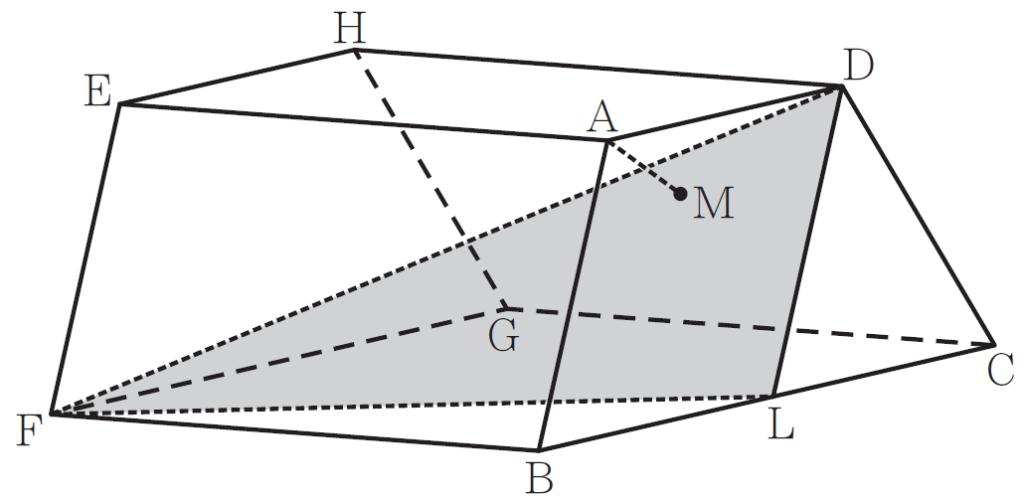
①は、線分DFの長さを求めろ、という問題。
簡単！△DLFで三平方で終わり！
って思う人が多いのですが、（２）の最初の問題文の中に、∠DLFは鈍角であると記述されてます。
つまり、この三角形では三平方が使えません。
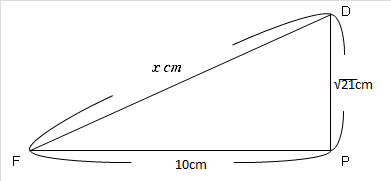
そこで、次の図をご覧ください。

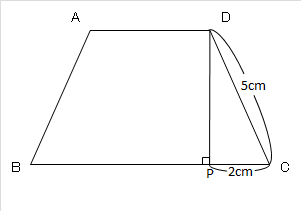
点Dから線分BCに垂線を下ろします。
BCとの交点をPとします。
等脚台形なので、PCの長さは２cmであることもすぐに判明するでしょう。
これで、線分DPの長さが出せますね。
DP＝\(\sqrt{~5^2-2^2~}＝\sqrt{~21~}\) cm
さらに次の図は、

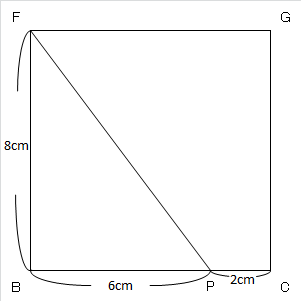
線分FPの長さを求めるために底面の正方形を再現しました。
三角形FBPを使えば三平方で一発ですね、というか、３：４：５ですね。
はい、FP＝１０cm
では、線分DFの長さを求めます。

• 

DF＝\(\sqrt{~10^2+(\sqrt{~21~})^2~}=\sqrt{~121~}=11\)cm

（２）②　解法

頂点Aから面DFLへ下ろした垂線の長さを求めろ、という問題。
この手の問題は、たいてい、立体の体積を求めて、面DFLを底面にして高さを\(x\)として方程式を作って答えにたどり着くのが定石。
では図をご覧ください。

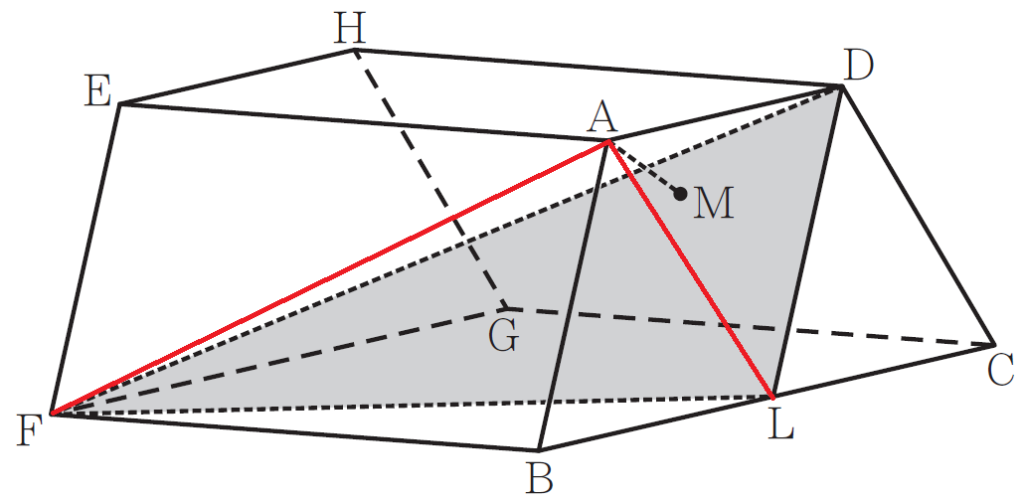
１：三角錐の体積を求める

赤線を２本引きました。
これによって、まず、頂点Fとする、三角錐F-ALDが完成します。
では、体積を求めます。
底面＝△ALD＝4×\(\sqrt{~21~}\)×\(\frac{~1~}{~2~}\)＝２\(\sqrt{~21~} cm^2\)
高さは、８cmなので、
体積＝２\(\sqrt{~21~}×８×\frac{~1~}{~3~}＝\frac{~16\sqrt{~21~}~}{~3~} cm^3\)

２：底面になる三角形の面積を求める

次に、△DFLの面積なんですが…
高校では、三角形の３つの辺の長さがわかっていたら、「ヘロンの公式」という公式を使って面積を出せます。
今回は、これを使わせてもらいます。
まずは公式の確認
三辺の長さが\(a,b,c\)の時、
①　\(\frac{~a+b+c~}{~2~}＝s\)とする。
②　面積＝\(\sqrt{~s(s-a)(s-b)(s-c)~}\)
DF＝11 cm、FL＝４\(\sqrt{~5~}\)、DL=５cmなので、
\(s=\frac{~11+5+４\sqrt{~5~}~}{~2~}＝(８+２\sqrt{~5~})\)
面積＝\(\sqrt{~(８+２\sqrt{~5~})(８+２\sqrt{~5~}-４\sqrt{~5~})(８+２\sqrt{~5~}-11)(８+２\sqrt{~5~}-5)~}\)
　　＝\(\sqrt{~(８+２\sqrt{~5~})(８-２\sqrt{~5~})(-3+２\sqrt{~5~})(3+２\sqrt{~5~})~}\)
　　＝\(\sqrt{~(64-20)(-9+20)~}\)
　　＝\(\sqrt{~44×11~}\)
　　＝\(\sqrt{~2^2×11^2~}\)
　　＝２×１１
　　＝２２ \(cm^2\)

３：AMの長さを求める

最終工程
\(
\begin{eqnarray}
２２×AM×\frac{~1~}{~3~}&=&\frac{~16\sqrt{~21~}~}{~3~}\\
\frac{~22~}{~3~}AM&=&\frac{~16\sqrt{~21~}~}{~3~}\\
AM&=&\frac{~16\sqrt{~21~}~}{~3~}×\frac{~3~}{~22~}\\
AM&=&\frac{~8\sqrt{~21~}~}{~11~}
\end{eqnarray}
\)

大阪府公立高等学校　一般入学者選抜　2021年度受験用 （公立高校入試対策シリーズ） [ 英俊社編集部 ] 価格：1430円（税込、送料無料) (2020/9/24時点)