（１）解法
実際の問題は、ホームページからダウンロードしたり、過去問を見てくださいね。では早速（１）の解説から。
四角形EACF は平行四辺形であることを証明しろ、という問題。
使える条件は、問題文に書かれている通り。
① △DAE ≡ △ABC
② AB // ED
③ △ABD はAB ＝ AD の二等辺三角形
④ F はE を通り辺AC に平行な直線と直線BD との交点
つまり、AC//EF
証明 開始
△ABD はAB ＝ AD の二等辺三角形なので
∠ABD＝∠ADB－①
AC//EFより平行線の同位角は等しいので
∠ADB＝∠EFD－②
AB // EDより平行線の同位角は等しいので
∠ABD＝∠EDF－③
①～③より、△EFDはED=EFの二等辺三角形。
よって、
EF=ED－④
さらに、△DAE ≡ △ABCより
DE=AC－⑤
④、⑤より
AC=EF－⑥
AC//EF、AC=EFより
一組の対辺が平行で長さが等しいので、四角形EACF は平行四辺形である。
（２）① 解法
辺BC の長さを求めろ、ということで、早速使える条件の確認から。
① AB ＝ 2 cm
② AC ＝ 6 cm
③ GA ＝ 2 cm
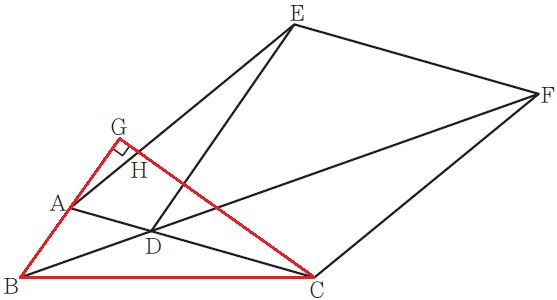
∠Gが９０°なので、最終的には赤線の△BCGを使ってBCを求めます。
そのためには、線分CGの長さを求める必要があります。そこで
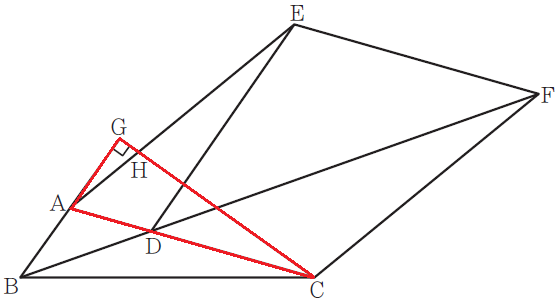
△ACGを使って線分CGを求めます。
線分CGの長さを求める
\(\begin{eqnarray}
AG^2+CG^2&=&AC^2\\
2^2+CG^2&=&6^2\\
CG^2&=&32\\
CG&=&4\sqrt{~2~}
\end{eqnarray}
\)
線分BCの長さを求める
\(\begin{eqnarray}
GB^2+CG^2&=&BC^2\\
4^2+(4\sqrt{~2~})^2&=&BC^2\\
16+32&=&BC^2\\
BC&=&4\sqrt{~3~}
\end{eqnarray}
\)
（２）② 解法
線分EH の長さを求めろ、という問題。
最終的には、これに気づけばOK！では図を。
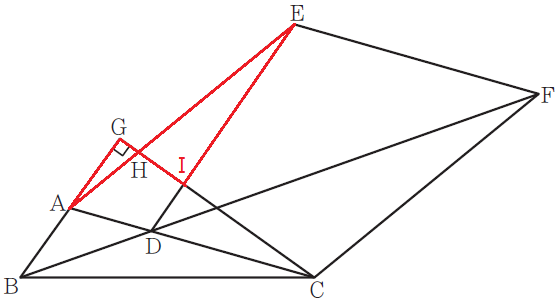
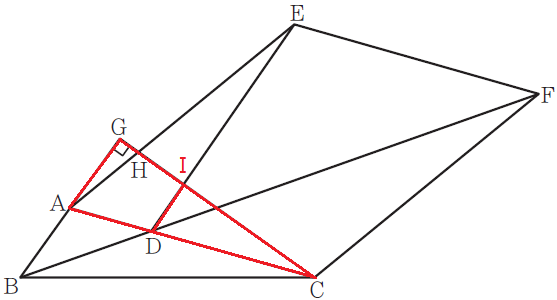
線分EDと線分CGの交点をIとしました。
GAは２cmであることがわかっていますので、線分EIの長さを求めて、相似比を求める。
最後は、その線分比を線分HA：線分HEに当てはめて線分EHの長さが出る、という公算。では早速やってみましょう。
まず、線分EIの長さを求めるために、次の図を使います。
△GACと△IDCは、AG//IDより、相似な三角形となります。
AD=AB=２cm、AC=６cmなので、DC=４cm
さらに、AG=２cmなので
\(
\begin{eqnarray}
CD：CA&=&DI：AG\\
４：６&=&DI：２\\
６DI&=&８\\ DI&=&\frac{~4~}{~3~}\\
\end{eqnarray}
\)
線分EIの長さを求める
\(\begin{eqnarray}
AC&=&ED\\
AC&=&6cm\\
EI&=&6-\frac{~4~}{~3~}\\
EI&=&\frac{~14~}{~3~}
\end{eqnarray}
\)
線分EHの長さを求める
△AGH∽△EIHなので
\(
\begin{eqnarray}
AG:EI&=&2:\frac{~14~}{~3~}\\
&=&6:14\\
&=&3:7\\
HA:HE&=&3:7
\end{eqnarray}
\)
これで、EHの長さが出ますね。
\(BC=AE=4\sqrt{~3~}\\
EH=4\sqrt{~3~}×\frac{~7~}{~10~}\\
EH=\frac{~14\sqrt{~3~}~}{~5~}
\)
（２）③ 解法
これは正直、どうやって攻めるねん！って感じでしたが、あることに気づいて速攻解決でした。ではその気づいた図をご覧ください。
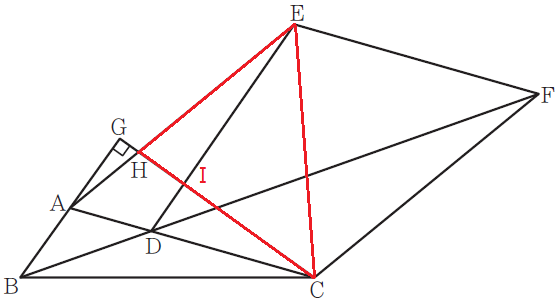
この赤線三角形の面積を求められたら、あとは、△EFCと面積比で仕留められることに気づいたんですね。
で、この問題、何を求めるんでしたっけ？
ん？四角形EHCF の面積を求めろ、ってか？
いけるな。
△EHCの面積を求める
\(△AGH∽△EIHなので、∠EIH=９０°\\
また、EIの長さは、\frac{~14~}{~3~}と、既に出てます。\\
IHの長さがわかれば、\\
CH×EI×\frac{~1~}{~2~}で面積が求められるので、IHの長さを求めます。
\)
GH・CHの長さを求める
\(CG=4\sqrt{~2~}\\
AD:DC=GI:IC=1:2\\
GI=4\sqrt{~2~}×\frac{~1~}{~3~}\\
GI=\frac{~4\sqrt{~2~}~}{~3~}\\
さらに、GH:IH=3:7なので\\
GH=\frac{~4\sqrt{~2~}~}{~3~}×\frac{~3~}{~10~}\\
GH=\frac{~2\sqrt{~2~}~}{~5~}\\
さらにCHの長さは、\\
CH=4\sqrt{~2~}-\frac{~2\sqrt{~2~}~}{~5~}\\
CH=\frac{~18\sqrt{~2~}~}{~5~}
\)
いよいよ△EHCの面積へ
\(面積=\frac{~18\sqrt{~2~}~}{~5~}×\frac{~14~}{~3~}×\frac{~1~}{~2~}\\
面積=\frac{~42\sqrt{~2~}~}{~5~}
\)
△EFCの面積を求めて、最終工程へ
四角形EHCFはEH//FCの台形です。
だから、△EHCの面積と、△EFCの面積を考える時、どちらも高さが同じであることに気づくかどうかです。
これに気づいた人は、△EHCと△EFCの面積比はEH:FCであることがわかります。
\(
EH:EC=\frac{~14\sqrt{~3~}~}{~5~}:4\sqrt{~3~}\\
EH:EC=7:10\\
よって面積は\\
7：10=\frac{~42\sqrt{~2~}~}{~5~}:△EFC\\
△EFC=12\sqrt{~2~}\\
四角形EHCFの面積は\\
面積=\frac{~42\sqrt{~2~}~}{~5~}+12\sqrt{~2~}\\
面積=\frac{~102\sqrt{~2~}~}{~5~}
\)
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1d1c1927.13c086fd.1d1c1928.0b40a76e/?me_id=1213310&item_id=20017893&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F6065%2F9784815416065.jpg%3F_ex%3D128x128&s=128x128&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
