問題
右の図のように、直方体ABCD-EFGHがあり、AB=AD=6㎝、AE=12㎝である。2点P,Qをそれぞれ辺BF,DH上にBP=DQ=3㎝となるようにとる。また、辺AE上に点RをCQ//PRとなるようにとる。
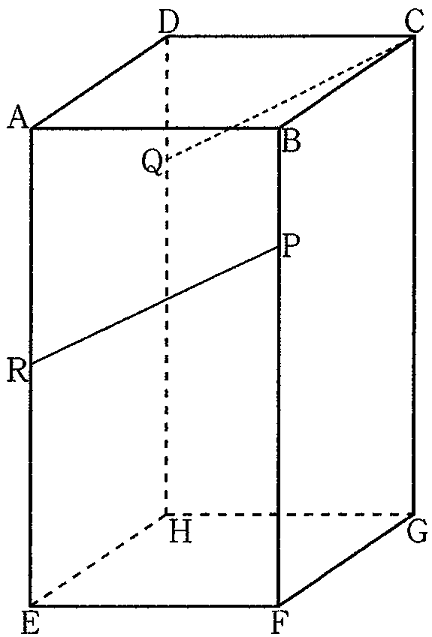
(1) 線分PQの長さを求めなさい。
押さえるべきポイントは
・BP=DQ=3㎝
PもQも3㎝上昇すると、BとDに重なるので、結局この問題は、線分BDの長さを求める問題だったということですね。
四角形ABCDは1辺が6㎝の正方形ですので、△ABDで、AB:AD:BD=\(1:1:\sqrt{~2~}\)より
BD=\(6\sqrt{~2~}\)=PQ
(2) 四角形CQPRの面積を求めなさい。また、直線CQと直線PRの距離を求めなさい。
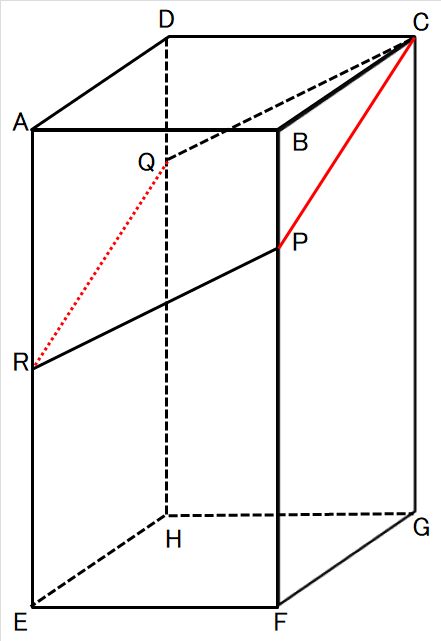
ということで、線分QRと線分CPを赤線でつないだ図になります。
この問題の難解ポイント・・・、それは・・・、
この四角形は、正方形じゃありませんから!ざんね~~~ん
古っ!
えっ?なに?って思われた方、忘れてください。
では気を取り直して、この四角形はひし形です。
なぜひし形なのか?
1:各辺の長さは全て\(3\sqrt{~5~}\)
えっ?正方形やん。
ちゃいまっせ!
正方形になるためにはもう一個条件が必要でっせ!
「角が90度」っちゅう条件ですがな。
えっ?でも角は全部90度やん!
ほなら90度とちゃう証明しまっせ!
△CPQに注目しましょか。
CQ=CP=\(3\sqrt{~5~}\)
PQ=\(6\sqrt{~2~}\)
ちゅうことで、この三角形は二等辺三角形になりますね。
えっ?ほんなら直角二等辺三角形やんか!
まぁまぁ、焦りなさんな。
直角三角形になるんやったら「三平方の定理」が成り立つよね。
左辺=\((3\sqrt{~5~})^2+(3\sqrt{~5~})^2=45+45=90\)
右辺=\((6\sqrt{~2~})^2=72\)
左辺≠右辺なので、直角三角形ではなかったですね。
つーことで、
ひし形確定
ほんで、どうやって面積求めんのよ!って方のために前へ進めます。
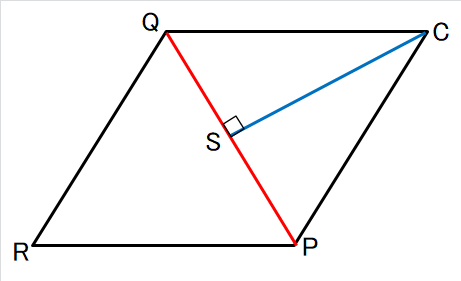
その直角三角形でないことを証明した三角形CPQに注目します。
Sは、頂点CからPQに引いた垂線とPQとの交点になります。
CQ=\(3\sqrt{~5~}\)
QS=\(6\sqrt{~2~}×\frac{~1~}{~2}=3\sqrt{~2~}\)
三平方の定理より
\(
\begin{eqnarray}
CS&=&\sqrt{~CQ^2-QS^2~}\\
CS&=&\sqrt{~(3\sqrt{~5~})^2-(3\sqrt{~2~})^2~}\\
CS&=&\sqrt{~45-18~}\\
CS&=&\sqrt{~27~}\\
CS&=&3\sqrt{~3~}
\end{eqnarray}
\)
つーことで、高さが求まったので、△CPQの面積を求めます。
\(\begin{eqnarray}
面積&=&6\sqrt{~2~}×3\sqrt{~3~}×\frac{~1~}{~2~}\\
面積&=&9\sqrt{~6~}
\end{eqnarray}
\)
△RPQ≡△CPQなので、面積も同じになります。
よって、
\(
9\sqrt{~6~}×2=18\sqrt{~6~}cm^2
\)
線分CQと線分PRの距離を求める。
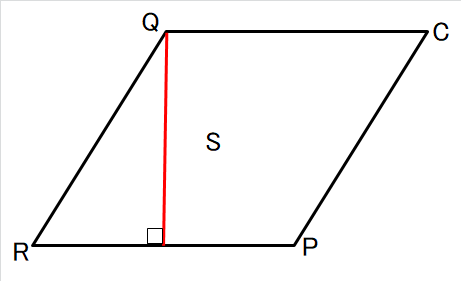
四角形の面積が求められたことによって、線分の距離はひし形の高さになりますね。
底辺×高さ$=$面積
\(
\begin{eqnarray}
3\sqrt{~5~}×高さ&=&18\sqrt{~6~}\\
高さ&=&\frac{~18\sqrt{~6~}~}{~3\sqrt{~5~}~}\\
高さ&=&\frac{~6\sqrt{~30~}~}{~5~}
\end{eqnarray}
\)
つーことで、2直線の距離は\(\frac{~6\sqrt{~30~}~}{~5~}\)ということになりました。
答え 面積 \(18\sqrt{~6~}cm^2\) 線分の距離 \(\frac{~6\sqrt{~30~}~}{~5~}cm\)
(3) 線分AFと線分PRとの交点をSとし、線分SFの中点をMとする。このとき、三角錐M-CQPの体積を求めなさい。
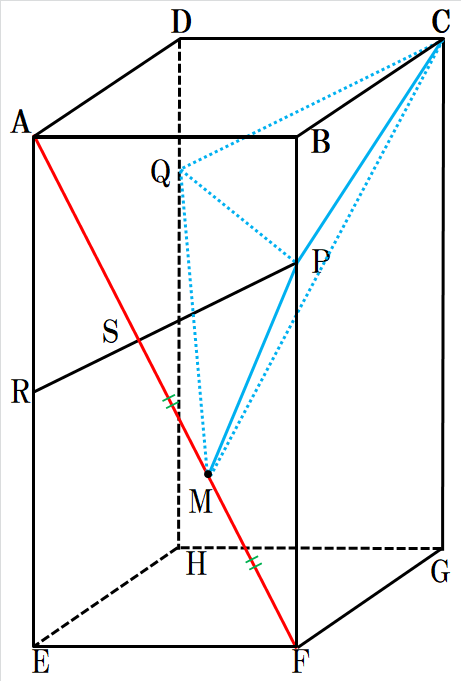
問題の通りに作図しますと、青線の通りの立体が浮かび上がりました。
正直、どこから攻めようか・・・悩みましたね。
悩んで悩んで、一つ前の問題に戻って、「なんでひし形の面積なんか求めさせたんや?」というところから考え直しました。
ひょっとして、ひし形の四角すいから体積を求めるのか?
そう思って、新たな線を引いてみました。
それが下の図です。
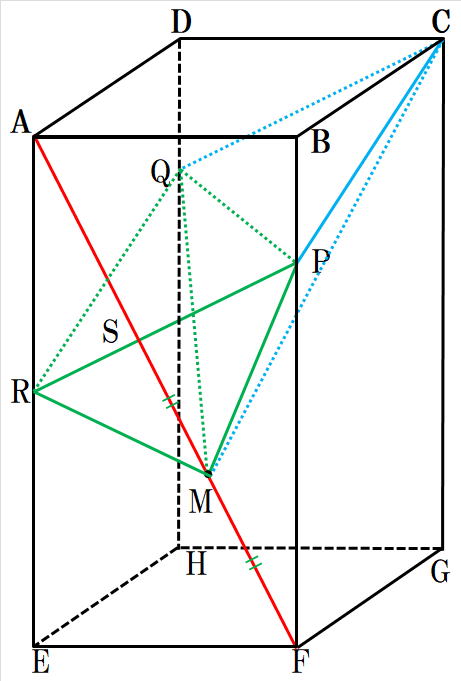
そうするとね、緑の三角錐が見えてきたんだよ。
面PQRとMとの距離さえ出せれば、体積出せるんやけどなあ・・・
ん?こ・こ・これは・・・
Qを頂点にして別の視点で見たら、高さが、線分DAと同じになるやんか!
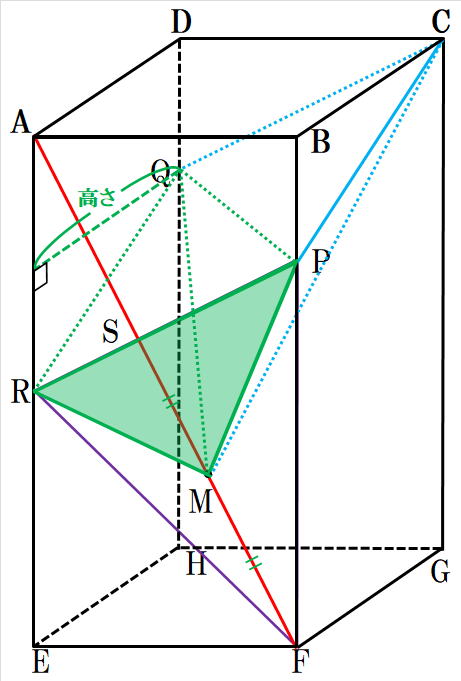
い・い・いけるぞ!これは・・・
よし!後は△PMRの面積や!
△PRFに注目しよか。
線分BP=3㎝なんで、線分PF=9㎝やね。
線分ABが高さになるね。6㎝ですわ。
ほんなら△PRFの面積=9×6÷2=27
△PMRの面積はその半分ということになるので、\(\frac{~27~}{~2~}cm^2\)となるね。
こ・こ・こいつ、動くぞ。
\(\frac{~27~}{~2~}×6×\frac{~1~}{~3~}=27\)
つーことで、体積は\(27cm^3\)となりました。
この立体と、三角錐M-CQPは、体積が同じになるので、\(27cm^3\)


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1d1c1927.13c086fd.1d1c1928.0b40a76e/?me_id=1213310&item_id=20011856&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F6058%2F9784815416058.jpg%3F_ex%3D128x128&s=128x128&t=picttext)
