普通に計算してしまうよね!
さぁ、出ました!
小学校5年生の問題!
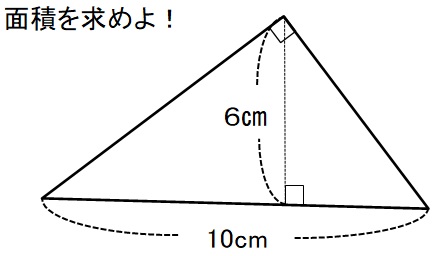
この三角形の面積を求めてください。
そんなん簡単やん。
10×6÷2=30㎠
はい!出ましたよ!
答えは・・・えっ?っという結果に
確かに計算したら30㎠ですよね。
正解!
って言いたいところなんですが・・・
「ブッブ~~~~~」
不正解です!
「えっ?何言うてんの!?アホちゃう!?」
ですよね。
実は、私もこの問題に正解できませんでした。
この問題の答えはズバリ!
こんな三角形は存在しない。
が正解です。
「はぁ~?意味わからんし・・・」
ですよね。
では解説です。
この三角形が存在しない理由はただ一つ
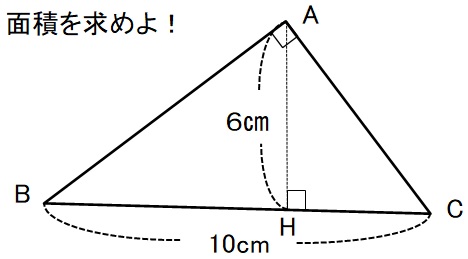
△ABCは∠A=90°の直角三角形です。
ということは、
ピタゴラスの定理
(三平方の定理)
が適用されます。
わかる人にはわかると思いますが、
上図で言うなら、
(AB)2+(AC)2=(BC)2
が成り立つわけで、
2乗+2乗=100が成り立つのは
62+82=102
ですよね。
この式から、
長い方のAB=8㎝
短い方のAC=6㎝
と判断されます。
この時、
「んっ?あれ?おかしいやん」
と気づけた人は大したものです。
そうです。ACの長さとAHの長さが同じになったんです。
「それがどうしたの?二等辺三角形やんか!」
確かにそう思いますよね。
でもよく見てください。
△AHCは直角三角形ですね。
つまり二等辺三角形であるはずがないのです。
だからこの三角形はこの世に存在しないのです。
ウソだと思うなら実際にこの三角形を作図してみるといいでしょう。
△ABCは作図できますが、線分AHを作図しようとすると5㎝目前で終わってしまうはずです。
つまり実際にはAHの長さは6㎝ではないんですよ。
逆に、線分AH=6㎝を保持するなら、線分ACの長さが6㎝よりも長くなってしまいます。
絶対に作図できないんです!
まとめ
三角形の面積を求める時、
- 実際に実在する三角形かどうかを確かめる
- その方法は、三平方の定理を利用する
- 三角形の性質を使う。
三角形の性質は、
- 短い辺+中くらいの辺>いちばん長い辺
- 短い辺+中くらいの辺<いちばん長い辺
のどちらかになっています。
もし、
短い辺+中くらいの辺=いちばん長い辺
だと、ただの直線になってしまいます。
子どもの解く問題にこんな問題は100%でないと思いますが、企業の入社試験だとこんなのが出るんですね。ちなみにこの問題は世界の大企業の入社試験だそうです。(知らんけど(笑))
最後に・・・
中学校や小学校で出てくる直角三角形は
3㎝、4㎝、5㎝ の直角三角形
もしくは
5㎝、12㎝、13㎝ の直角三角形
しか出ません。
何かの参考になればと思います。
最後までお読みいただきありがとうございました。



