円すいの体積を求めたり表面積を求めたり。
挙句、展開図にしたおうぎ形の中心角を求めたり。
テストって容赦ないですよね。
本来のやり方で解いたら結構時間もかかるんですが、
実はすぐに解決できる公式があるので紹介したいと思います。
難しい公式だとわかりずらいですが、この公式は超簡単!
是非覚えて使ってください。
ちなみに私は100%使っています。
できると思うにせよ、できないと思うにせよ、そのとおりになる。
円すいの展開図の中心角はこうやって解く!
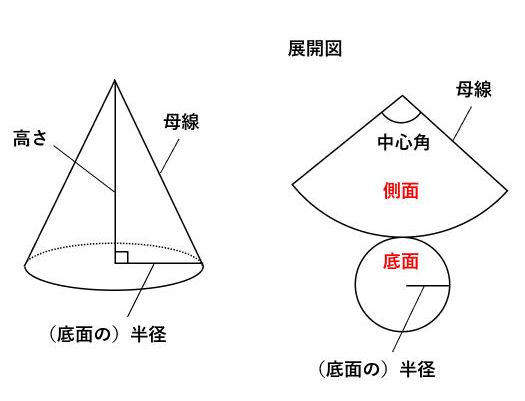
まず公式からご紹介
円すいの側面(おうぎ形)の中心角=\(360°×\frac{底面半径}{母線}\)
です。
導き方に興味のない方は、次の
円すいの側面積の公式
に飛んでください。
展開図の扇形の中心角を導く!
では導きたいと思います。
導き方ですが、おうぎ形の弧の長さが、
母線を半径とする円の円周の何分のいくつになるのか?
という割合から公式に持って行きます。
まず、弧の長さから求めますが、
弧の長さ=底面の円の円周
ということがわかっていますので、
底面の円周の長さを使います。
\(半径×2×\pi=2\pi半径\)
次に母線を半径とする円の円周の長さを求めます。
\(母線×2×\pi=2\pi母線\)
弧の割合を求めます。
\(
\begin{eqnarray}
弧の割合&=&\frac{2\pi半径}{2\pi母線}\\
&=&\frac{半径}{母線}
\end{eqnarray}
\)
これで弧の割合が出ました。
中心角の大きさ=弧の割合×360°になりますね。
よって、
\(360°×\frac{半径}{母線}\)
になります。
展開図扇形の面積はこれで解ける!
では、側面積の公式を公開します。
こちらです!
\(母線×底面半径×\pi=側面おうぎ形の面積\)
ここでご注意!
「表面積」を求めなさい、と言われたときは、
底面の円の面積も必ず足してくださいよ!
これを面倒だという人のために
私が考えた「表面積」の公式がこれです!
\((母線+底面半径)×底面半径×\pi=円すいの表面積\)
表面積の導き方は、興味のある方のみご覧ください。
展開図扇形の面積(円すいの側面積)の公式を導く!
では、導いてみましょう!
中心角の公式を最初に導いていますね。
\(中心角=360°×\frac{半径}{母線}\)
これです。
これを使って公式を導きます。
おうぎ形の面積の公式は
\(半径×半径×\pi×\frac{中心角}{360°}\)
ですよね。
今回、半径となっている部分は「母線」に置き換わります。
それから、
\(\frac{中心角}{360°}\)
の部分を割り算に変換します。
\(中心角÷360°\)
に直します。
では、改めて公式に当てはめてみます。
\(
\begin{eqnarray}
側面積&=&母線×母線×\pi×360°×\frac{半径}{母線}÷360°\\
&=&\frac{母線}{1}×\frac{母線}{1}×\frac{\pi}{1}×\frac{360°}{1}×\frac{半径}{母線}×\frac{1}{360°}\\
&=&母線×半径×\pi
\end{eqnarray}
\)
ふ~う、
何とか導けましたね。
ではもう一つ、
私が導いた「表面積」の公式はどうやって導いたのか、
これはもう察しがつきますか?
\(
\begin{eqnarray}
表面積&=&母線×半径×\pi+半径×半径×\pi\\
&=&(母線+半径)×半径×\pi
\end{eqnarray}
\)
要するに、側面積と底面積を足した式を
共通因数で因数分解しただけなんですね。
私は結構この「自分流」の円すい公式を使っています。
皆さんも良ければ使ってみてください!
さらに、もっといろんな公式を知りたい!
という方にお勧めの本があります。
ちょっと高価な本ですが、高校入試に必要な公式がほぼ収録されています。
つまり、これ1冊あれば、公式で困ることはありません!
「塾技」という名前の通り、塾で教えてくれる公式が載っています。
是非ご購入ください。